Robust Quadrupedal Locomotion using RL

Project conducted at the Stoch Lab, RBCCPS IISc Bangalore as a part of my Bachelor’s Thesis, under the guidance of Prof. Shishir Kolathaya.

Project Abstract

Quadrupedal robots have the potential to be used in a wide range of applications, including search and rescue, surveillance, and exploration. However, the high number of degrees of freedom and the complex interaction between the quadrupedal robot and the environment make it difficult to model their motion. Reinforcement Learning (RL) based control strategies have shown promising results for quadrupedal locomotion. However, these strategies are often tested in simulation environments and are not robust to real-world conditions. In this project, we aim to develop a robust RL-based control strategy for quadrupedal locomotion on sloped terrain. We use the StochLite quadruped robot for our experiments.

Hardware Description of StochLite

StochLite is a 3rd generation quadruped robot developed at the Indian Institute of Science, Bangalore. It features a 12-DoF design with 3D printed parts and off-the-shelf components, offering easy modifications and maintenance. Its open-frame design facilitates easy upgrades and maintenance, and the sensor suite is comprehensive. It includes an Inertial Measurement Unit (IMU), six Time of Flight (ToF) ranging sensors, integrated joint-encoders, and motor current sensors within the servo motors. The central computing power comes from a Raspberry Pi 3B, which communicates with the motors using the RS485 protocol via an FTDI converter chip. ToF sensors communicate with an Arduino Nano, which relays the data back to the Raspberry Pi. This modular setup allows for the exchange of electronic hardware components to adapt to specific task requirements.

StochLite’s legs feature a 3-RRR serial linkage architecture, with each leg having three actuated joints for hip abduction/adduction, hip flexion/extension, and knee flexion/extension. The design of the thigh and shank is optimized for a large workspace, enabling the robot to navigate complex terrains with ease. The full 180° range of motion in the legs allows for configuration changes on the fly without disassembly. Even the feet of StochLite are a marvel of 3D printing. They are crafted using a combination of materials, with the end point contact made from flexible TPU 95A for traction and the structure built from PLA for durability. This unique combination ensures the robot can maintain traction on various terrains.

To bridge the gap between simulation and reality, a Unified Robot Description Format (URDF) model for StochLite was created using measurements and weights of each part. This painstaking process, which involved estimating inertia based on shape and mass, greatly improved the accuracy of the robot’s behavior in the Pybullet simulator.

Software Architecture

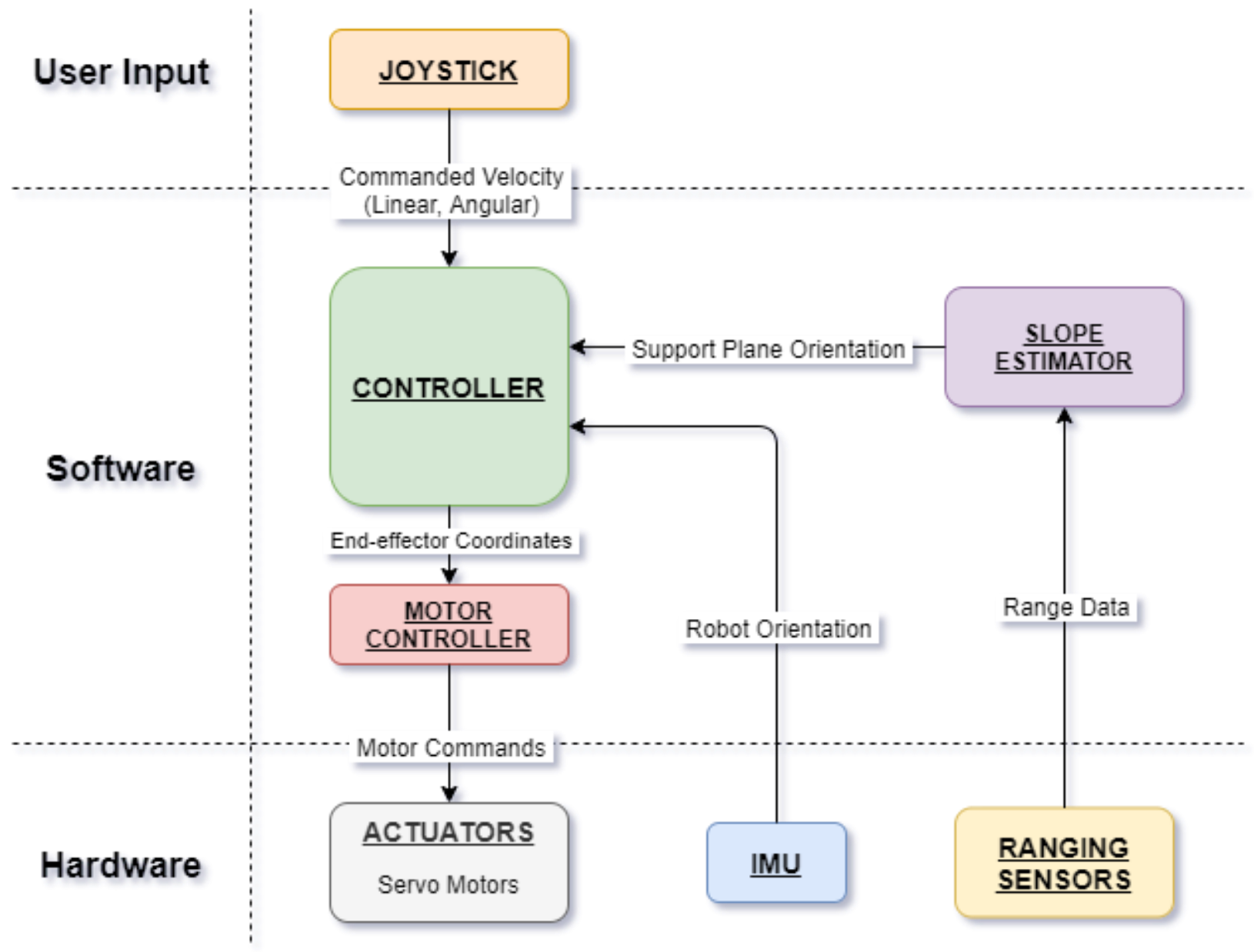
A block diagram depicting the different components and their interconnections is shown in the figure above. The controller component coordinates the functions by reading data from sensors, determining the control actions to be applied, and finally forwarding the control commands to the actuators. Sensor data is obtained from an Inertial Measurement Unit (IMU) and multiple ranging sensors placed on the robot. Data from the IMU is filtered and processed to obtain the pose of the body and data from the ranging sensors is used to determine the relative slope of the ground with respect to the robot body. These sensor data along with user inputs from a joystick are used to control the actions of the robot.

Reinforcement Learning Framework

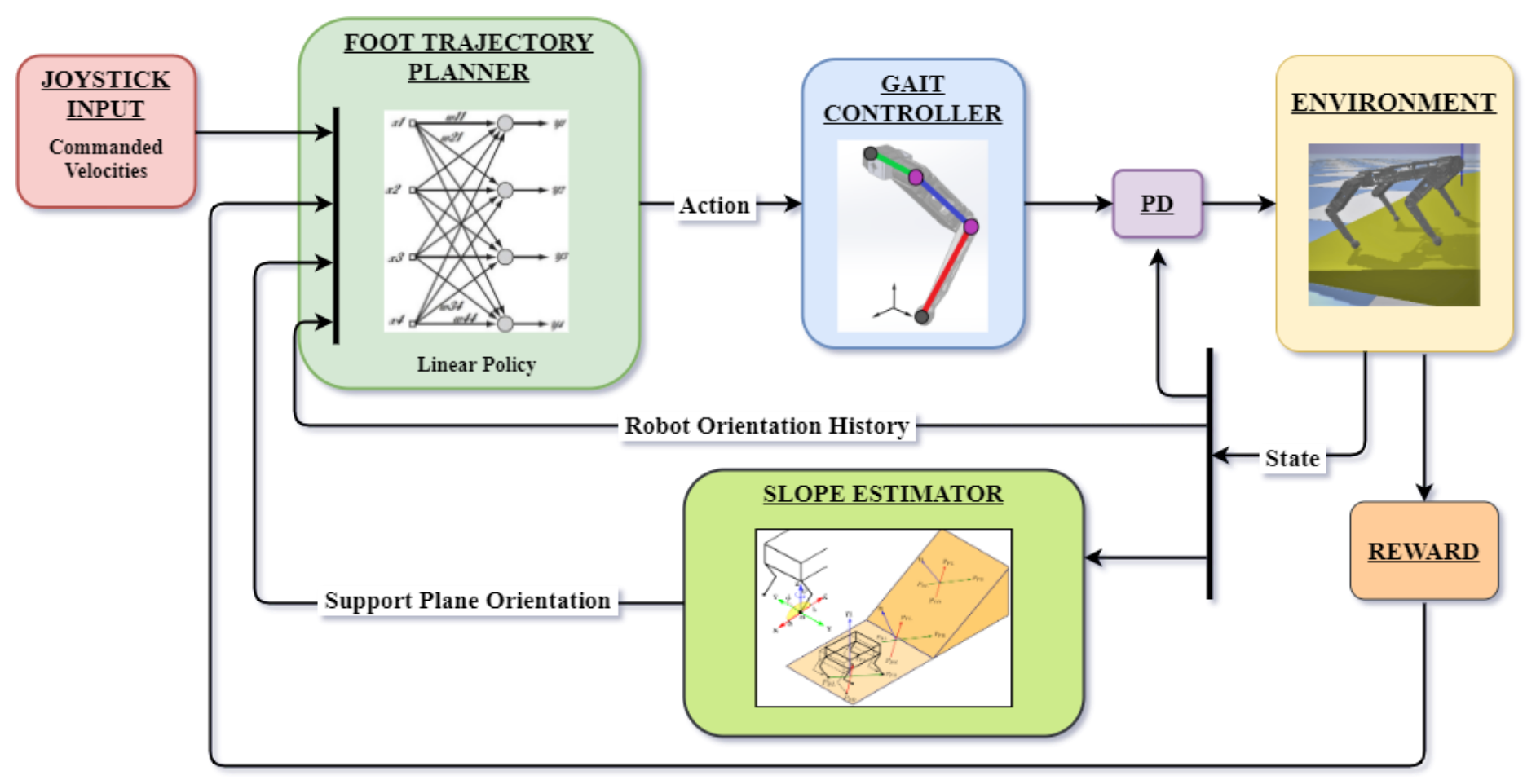
The sloped terrain locomotion is formulated as a reinforcement learning problem, with an observation space, action space and a reward function. Our policy π is a linear transformation that maps the observation vector to the action vector.

The observation space considered for this problem forms an 11-dimensional state vector, which consists of robot orientation (roll, pitch and yaw) for three time steps t, t-1, t-2, and the estimated roll and pitch of the slope at time step t. Having the orientation data of previous time steps helps in deploying the policy on the robot - it helps to take into account the latency caused by the communication between the micro-controllers and sensors on-board the robot. The robot base orientation and terrain slope parameters are highly relevant observations for locomotion on rough terrain. The base orientation is measured directly by the IMU, while the terrain slope parameters are estimated by the range data from the six ToF sensors on the robot.

The action space is a 20-dimensional vector which consists of five transformations for each of the four legs. These transformations transform the 2D semi-elliptic end-foot trajectories in a 3D work-space for each of the four legs. A semi-elliptic trajectory is chosen to allow for computationally simple implementation of the controller. The transformations consist of the variation of the length of the major axis of the semi-elliptical trajectory (footstep length), rotation of the trajectory about the Z-axis (steer angle), and the translation of the trajectory along the X, Y , and Z axes. All the transformations are defined in the local leg frame of reference. After the corresponding transformations, the obtained end foot trajectory is passed to an inverse kinematics solver to get the joint angles.

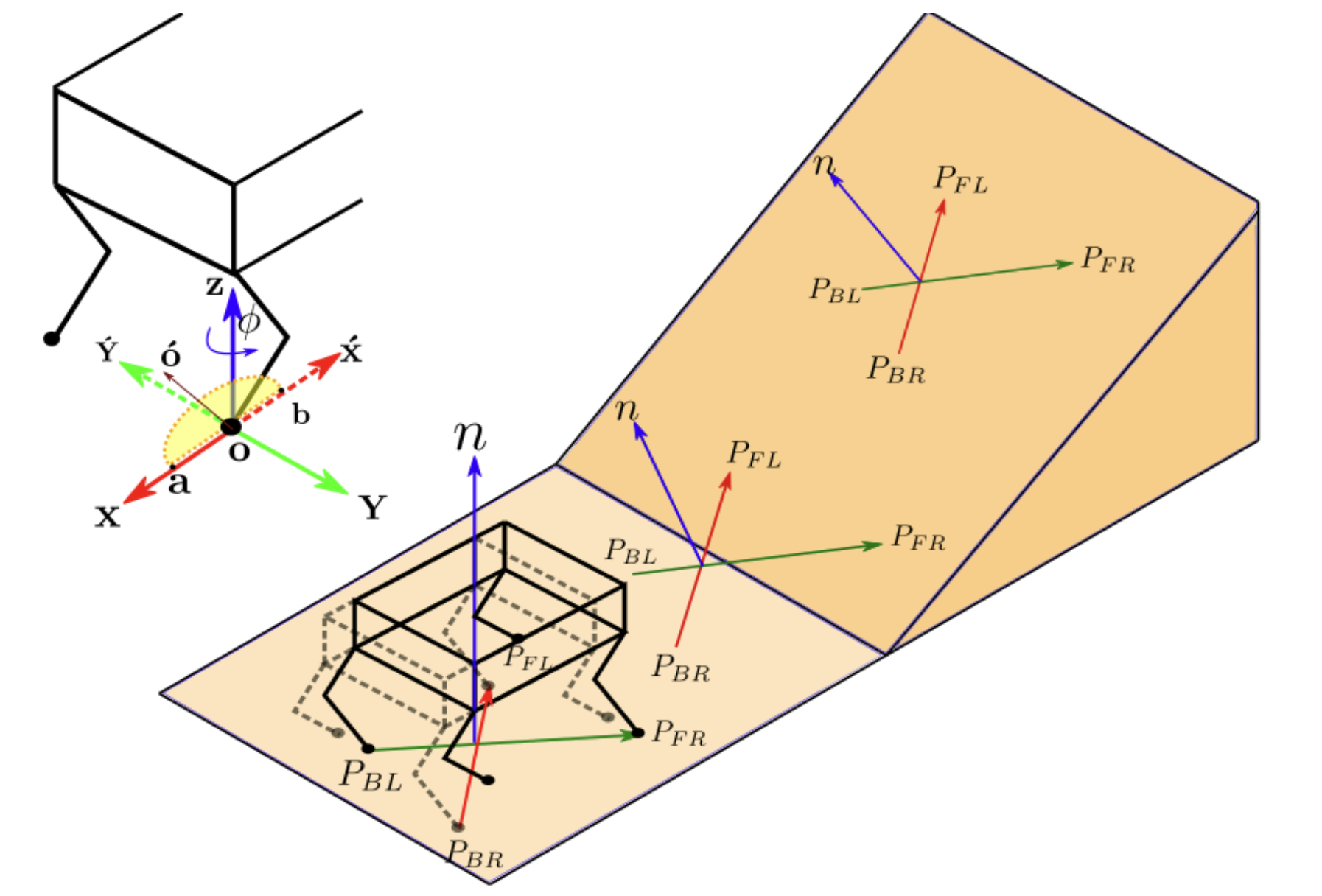
The orientation of the robot and the support plane (terrain) is used to obtain the trajectory parameters. The orientation of the robot body can be directly obtained from the IMU. The terrain slope estimation in simulation uses a foot-contact approach - after the foot contact is detected, the joint angles are sent through a forward kinematics solver to get the coordinates of the foot contact, subsequently getting the equation of the support plane. In the real world, the terrain slope is estimated using the range data from the ToF sensors.

Transitioning from a stand-still position to a certain linear velocity, and transitioning from flat uniform terrain to rough terrain are the two major transitions that can be observed in the general operation of a quadruped. The walking control strategy on Stochlite was designed to accommodate for these transitions. A sudden transition in linear walking affects three of the five trajectory parameters - the footstep length, and the X and Z shift of the trajectory. Offsets were added to these parameters based on the joy-stick command velocity and the terrain estimation to aid in the stability of the robot.

The learning algorithm used for training Stoch-Lite is Augmented Random Search (ARS). This algorithm is designed for finding linear deterministic policies. The policy is parameterized as a linear transformation of the observation vector. The policy is trained on the basis of the joy-stick input. Two types of input velocities can be defined from the joy-stick - the translational velocity of dimension two, and a rotational velocity of dimension one. The translational velocity command provides the velocity in the x and y direction, while the rotational component provides the angular velocity of the torso respectively. The joy-stick command is defined in the training algorithm as a function of the number of steps in an episode and added as an offset to the actions corresponding the footstep length of the robot. For the first 20% of the steps, the command velocity is zero. This simulates the stand-still step-in-place (0 footstep length) of the robot. For the remaining length of the episode, the command velocity is a ramp input. Accordingly, the robot must walk from a zero velocity mode to a maximum linear velocity mode. The reward is structured accordingly. The reward function for the policy is designed such that the robot is encouraged to keep moving forward with the velocity commanded through the joy-stick, irrespective of the underlying terrain.

The open-source physics engine, PyBullet was used to simulate and train the agent. Anasynchronous version of Augmented Random Search with 15parallel agents was used to speed up the training on the robot.The rough terrain for training the robot wad aprroximatedby using slopes of varying inclinations. The inclinations are discretized at 0°, 5°, 7°, 9°, 11°, 13° and 15°. The inclinations aremeasured with respect to the x - y plane rotating aboutpositive Y axis, in a pure pitch uphill fashion. The robotis spawned on the flat ground, at some distance from theinclination, and then as the commanded velocity is increased, it should walk towards the inclination and start climbing. This helps in training the robot to walk on flat ground, and then transition onto a rough terrain sloped ground. After every policy update, an inclined slope is sampled from the above mentioned range. Instead of starting with a random policy matrix, we used a guided initial policy to give a warm start to our ARS algorithm for policy exploration. We chose a few sets of hand- tuned fixed action values with reference to the telescopic strut strategy and simulated these actions to collect corresponding observations from the environment. Then, we did supervised learning to map the observations with the hand-tuned action values to obtain our guided initial policy. With our current action framework, it is quite intuitive to come up with such sets of action values that can perform fairly better than a random initial policy which significantly reduces the number of training iterations.

Results